

Figure 1
The first step seemed to me to be to isolate and assign numerical values to the
lines which form the simple wave. Thirteen discrete line types comprise any
simple version of the wave. These thirteen lengths are displayed on and off
grid in Figure 2:
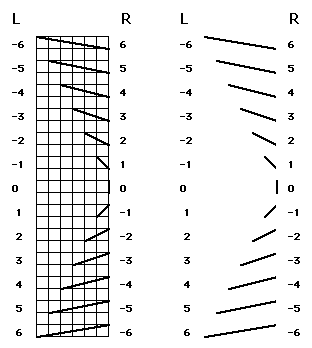
Figure 2
As these lengths are always discrete units, we can assign to them values which
are ascending integers. The values of Figure 2 allow a quantification of line
length. To quantify the degree and direction of skew of individual lines, one
direction of skew is designated as positive, giving lines skewed in that
direction positive values. Lines skewed in the opposite direction are given
negative values. This gives values adequately preserving and quantifying line
length and direction of skew. The values labeled L in Figure 2 are used for
the left side of a simple wave while the values labeled R, which are the same
values with their sign reverse, are applied to the right side of any
simple wave. The sign is important only in combining values across scales but
is ignored in the final graphing of combined values, either set of values may
be applied to either the right or left side. However, whichever schema is
chosen must then be followed throughout. Figure 3 represents the version of
these values that we have used for the simple graph.
In the same fashion that similar structures on the right and left side of the
wave are given equal values of opposite signs in order to preserve their
symmetry, so too the symmetry between the top half and the bottom half of the
wave is preserved by a similar operation: The midpoint of the wave is a switch
over point where signs are reversed for the 32 values that are the last half of
the wave. This move preserves symmetry as those values switch from one side of
the wave to the other. This is the famous "twist" that Watkins has claimed is
not a rational move. More on this further on.
Take a look at the values that enter into the valuation of skew:
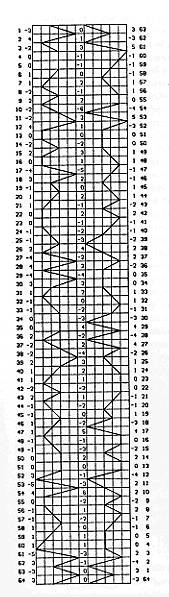
Figure 3
It is important to note that the valuations in Figure 3 are valuations of
the simple wave on the smallest scale of a single complex wave. The relative
proportions of the three levels in the complex wave are preserved and
quantified by multiplying the valuations of the linear scale in the appropriate
way. To assign a value to a position on the trigramatic scale, the valuation
of that position on the linear scale (Figure 3) is multiplied by three because
the trigramatic scale is three times larger than the linear scale. In a
similar manner, the hexagramatic positions are assigned a valuation by
multiplying their linear-level valuations by six, again because the
hexagramatic scale is six times larger than the linear. Figure 3 uses the value
scheme in Figure 2 and is the version of value assignments we have used in all
our calculations. For a graphic representation of the relation of the three
levels in a complex wave see Figure 11.
Note that in Figure 3 all parallel lines, regardless of the distances
separating them, reduce to zero. Thus, while the operations discussed so far
have allowed quantification of skew direction, proportional ratios of the wave
parts, and the degree of departure from the parallel state, they have not
provided a quantified account of the fluctuating distances between the two
parameters of the wave. The procedure for obtaining these values is similar
to, but distinct from, the procedures outlines above.
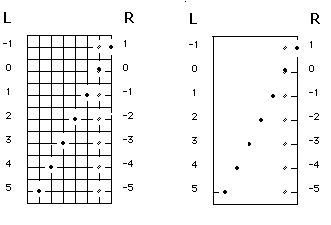
Figure 4
Figure 4 shows the seven types of divergence, congruence, and overlap which
points in the simple wave may display. The two possible assignments of
positive and negative numbers are shown to the right and left sides in Figure
4. We have chosen to use the right-hand schema to preserve the intuition that
overlap tends to carry a situation toward the zero state rather than away from
it.
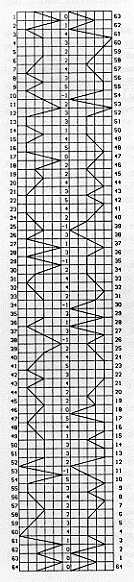
Figure 5
Figure 5 shows the values this series of point assignments generates when
applied to the simple wave. When the valuations for skew, parallelism, and
relative proportion have been combined in the manner detailed above the
following graphic evaluation of the simple wave is the result:
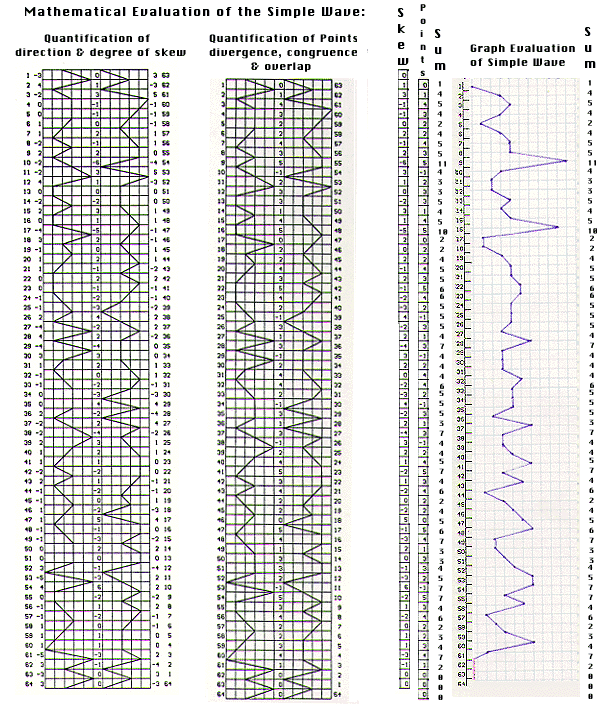
Figure 6
Figure 6 brings us to the crux of the Watkins Objection. Watkins is
challenging the method by which the simple bi-directional wave of Figure 1 is
converted into the figure at the extreme right in Figure 6.
This is a central objection since that figure is the modular foundation of the
complex wave and of the fractal hierarchy that is built upon it. Let's take a
look at the simple wave and its mathematical reduction side by side. The
reduction preserves all of the most important intuitions that guided the
construction of Novelty Theory; in particular it preserves the idea that the
area of closure in both the simple and the complex wave should quantify as
zero. It is this unique zero point that gives the theory its eschatological
properties and it was the centrality of this concept that lead to naming the
software "Timewave Zero".
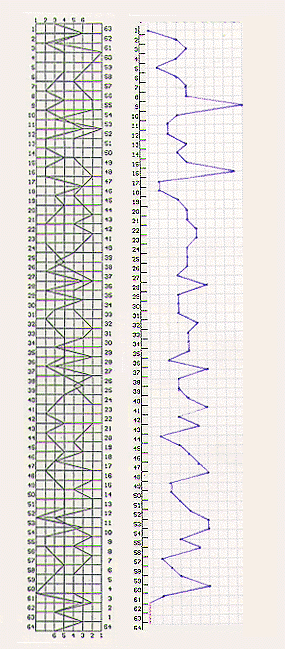
Figure 7
The skew components maintain their symmetry relative to the center of the wave
by being numerically identically but of opposite sign.
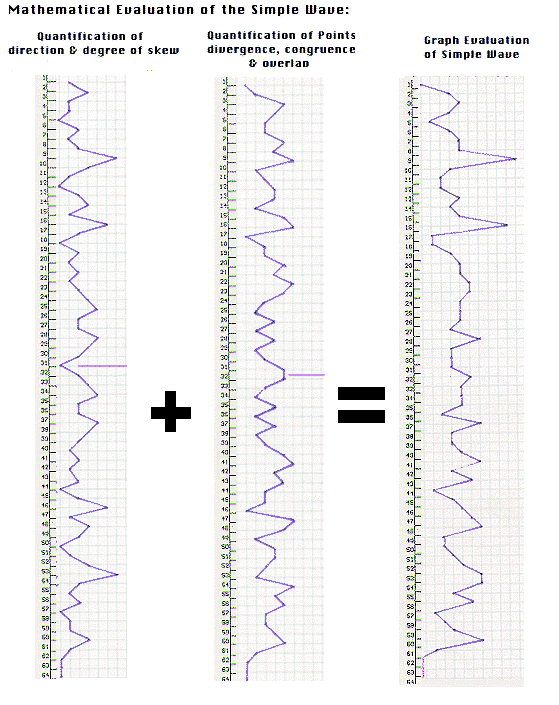
Figure 8
The point evaluations also have symmetry.
The axis of symmetry of both graphs is indicated by a violet line. The one
position offset of the two sets of symmetrical data points gives rise to the
asymmetry of the final combined valuation. This offset occurs because Skew
etc. is an evaluation of one portion of the wave to a portion directly across
from it, while Point/Distance etc. is an evaluation of the transition between
one portion of the wave and the portion next to it.
In order to fully understand the Watkins'' Objection it is necessary to
construct a mathematical evaluation of the simple wave without the inclusion of
the "twist" that Watkins is opposed to. When this is done the follow
mathematical reduction takes place:
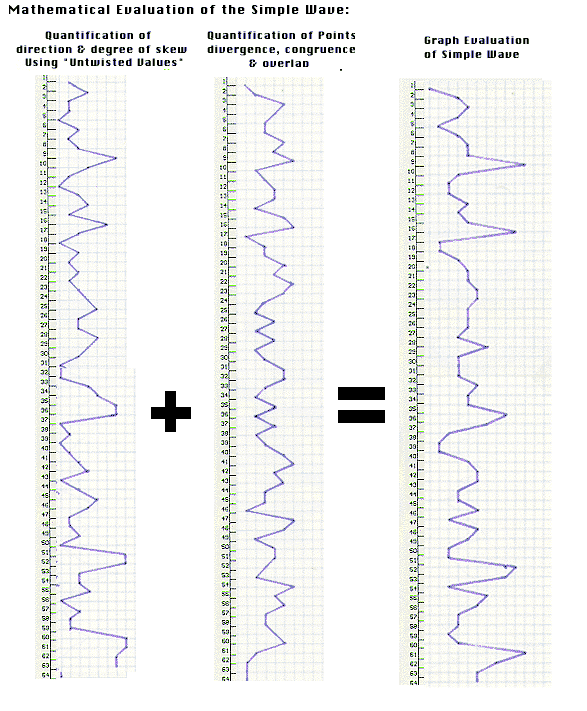
Figure 9
We are now in a position to place the simple wave, the original valuation and
the valuation implied by Watkins' Objection side by side for comparison.
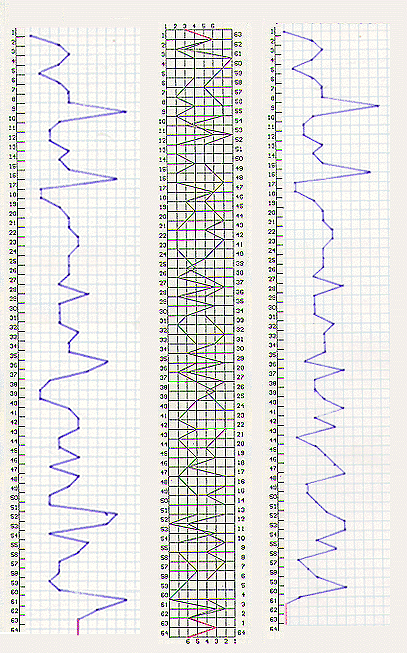
Figure 10
When this comparison is carried out I maintain that all basis for Watkins'
objection to the "twist" is revealed as unfounded. With the twist removed as
in the valuation to the left of the simple wave it is clear that the reduction
fails to reflect a primary intuition of Novelty Theory; that closure will
quantify as zero. This original and primary intuition is not preserved in the
Watkins' valuation. Examine instead the valuation on the right, this is the
standard valuation, generated by the inclusion of the "twist" in the method of
evaluating the simple wave. this method preserves the intuition that closure
will always quantify as zero. Hence the original method is to be preferred and
the Watkins' Objection is answered.
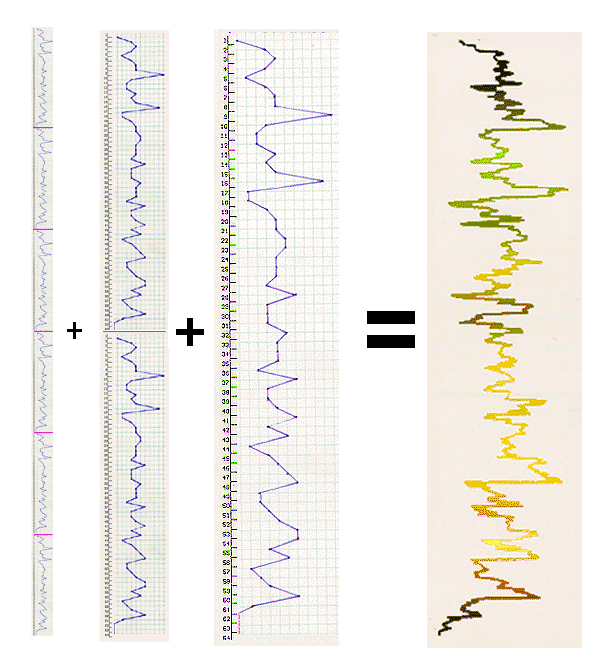
Figure 11