(1) The Linear Forward Wave Vector                                                      [skip to next]

The parameter is introduced by defining the straight line in terms of a point , a vector , and a parameter t. Refer to Fig. 5 and locate the vectors 0A, AB, and 0P. We have already defined vector AB in equation [12] as the forward wave vector  (Eqn [16]), which establishes a direction for our line segment. Vector 0A is in standard position (tail positioned at the coordinate system origin), so that it is defined by the position of its head at point . Vector 0P is the variable or moving vector and, like the moving pencil point, its head traces the path of the straight line that we are interested in. Let us rename vector 0P as the linear forward wave vector , and since it is in standard position (tail at the origin so that it is defined by the coordinates of its head), it is described mathematically by the following expression:
 

              [24]

in which  are the variable coordinates of the vector head. This vector can also be expressed as the sum of vectors 0A and the forward wave vector  as follows:

              [25]

 Vector 0A in standard position is expressed as 

and from equation [16]  

so that equation [25] can now be expressed as:

             [26]

with the parameter t having a range:  over the x domain 

Equation [26] can now be solved for x and y_F, the general coordinates of the vector , to determine the parametric equation of the line describing the motion of the forward wave. Solving for x and y_F yields the following parametric equations of the line:

              [27]

            [28]

Solving [27] and [28] for the parameter t we get:

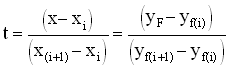             [29]

These expressions for the x and y variables in equation [29], are the standard form of the line equation, and show that the parameter t behaves as an interpolation operator for the x and y coordinates of the forward wave line segment. Rearranging terms for the variables in equation [29] leads to the slope y-intercept form of the straight-line equation, which is a convenient form of expression for the line segment of interest in this development. The slope y-intercept form of the line is determined by solving [29] for the variable , which results in the expression:

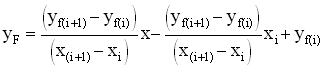             [30]

Define:  and  , so that [29] becomes:

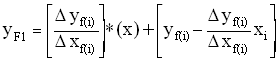             [31]

 
which is the slope y-intercept form of the forward linear wave line segment, where the slope is  , and the intercept is . Equation [31] is the vector-derived expression that is used to generate the linear forward wave over the domain . This forward wave vector generation process is now repeated for the reverse wave vector.

 
(2) The Linear Reverse Wave Vector

The process for generating the vector parametric equations for the reverse wave segment is the same as for the forward segment, but with a vector that has the opposite sense (opposite flow) of the forward wave vector. Again, refer to Fig. 5 and find vectors 0C, CD, and 0Q. Vector CD has already been defined in equation [17] as the reverse wave vector, . Vector 0Q, like vector 0P, is the moving variable vector (tail is fixed, but head moves and traces the line of interest) which will trace the path of our reverse wave line segment. We now rename 0Q as the reverse wave-generating vector and since it is in standard position it can be expressed as:

             [32]

In which  are the variable coordinates for the head of . Expressing  as the sum of 0C and the parameter scaled , we have:

             [33]

Substituting for 0C and  we have:

       [34]

Solving for x and y_R yields the following parametric equations of the line:

         [35]

             [36]

Solving for the parameter t we get:

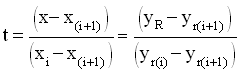         [37]

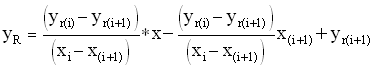         [38]

Define:  and  , so that [38] is expressed in the slope y-intercept form of the linear reverse wave line segment. Notice also that , an identity that will be exploited later. For the slope y-intercept form of [38] we substitute the delta () expressions and collect terms:

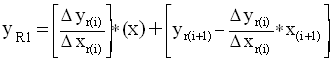             [39]

Equations [31] and [39] constitute the defining expressions for the linear forward and reverse waves respectively, and equation [11] provides the correct value for the subscript i in equation [39]. These equations can be either expanded into the trigramatic and hexagramatic bi-directional waves (TBW and HBW) directly, which are then combined to form complex waves; or they can be first combined into a linear complex wave, then expanded into the trigramatic and hexagramatic complex waves. Either of these two procedures will lead to the same final 384 number data set, but the latter is a more streamlined process that eliminates several operational steps. The complex wave is defined here, as any wave that is a linear combination of one or more bi-directional waves, and is not expressed in bi-directional form. So now let us continue with the process of wave combination, beginning with the linear bi-directional (forward and reverse) wave.

(3) The Linear Complex Wave

Before beginning the mathematical development of the linear complex wave, let us first establish the procedure for forward and reverse wave combination.

Definition 4:
In order to produce forward and reverse wave endpoint (node) closure at zero (0) value, the forward and reverse waves must be subtracted from one another to yield zero valued endpoints for the combined simple wave. In order to maximize the number of positive values for the resultant combined wave, the forward wave is subtracted from the reverse wave.

The linear complex wave is therefore produced by subtracting equation [31] (the forward wave line segment), from equation [39] (the reverse wave line segment). The combined or complex linear wave is thereby expressed as:

             [40]

 
Replacing the expression  with the right hand sides of equation [39] and [31], we get:
 

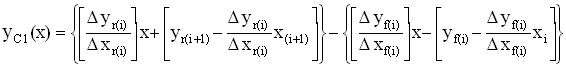             [41]

and combining like terms and rearranging equation [41] gives us:
 
 

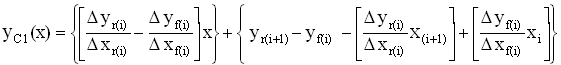          [42]

Using the identity shown previously, , equation [42] is reduced to the defining equation for the linear complex wave:

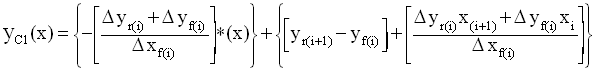     [43]

Where yC1(x) is the linear complex wave function and the delta ( ) functions defined as:

Which is the change in the linear reverse wave dependent variable yr over the x domain of 

,

Which is the change in the linear forward wave dependent variable yf over the x domain of 

Which is the change in the independent variable x over the domain of the linear complex wave line segment, 

Substituting the domain endpoints, x_i and x_(i+1) for the x variable, equation [43] reduces to:

             [44]

             [45]

 
Which confirms what we observe at the linear wave line segment endpoints, and validates equation [43]
 

[continue]             [results & conclusions]             [index]             [hyperborea]             [back]