
According to McKenna [10] the Trigramatic wave is an expression of the trigram pair that form each I-Ching hexagram. Since each hexagram has a pair of trigrams, a Trigramatic Wave pair is constructed such that the two trigramatic waves are placed end-to-end (concatenated), and have the domain (x-axis range) of six simple wave cycles. The Trigramatic wave is also viewed as having a value of three times the linear wave, since a trigram consists of three lines (trigram = 3 x 1 lines). Similarly, the Hexagramatic wave is viewed as an expression of the unity of each hexagram, and is constructed so that a single hexagramatic wave occupies the domain of six simple waves cycles (six lines to a hexagram), or two trigramatic wave cycles (two trigrams to a hexagram). Additionally, since the hexagram contains six lines, the hexagramatic wave is seen as six times as large as the simple wave (hexagram = 6 x 1 lines, and hexagramatic wave = 6 x 1 simple waves).
This Tri-Level Complex Wave is described as having the same three nested levels of expression as exhibited by an I-Ching hexagram. The top level is the Hexagramatic Wave, or hexagram as a whole, which contains the two lower levels, two Trigramatic Waves and six Simple Wave cycles. The mid level of expression is the Trigramatic Wave, which contains the six Simple Wave cycles below and is contained by the one hexagramatic cycle above. The bottom level of expression is the linear wave, having six simple wave cycles that are contained within two trigramatic wave cycles and one hexagramatic wave cycle.
If we were to look at the complex wave as analogous to
some physical wave, be it electromagnetic or acoustic, then this tri-level
wave structure could be viewed as harmonic in nature. The hexagramatic
wave would then correspond to the wave fundamental or 1st harmonic, the
trigramatic wave would correspond to the second harmonic (2x the fundamental
frequency), and the linear wave would correspond to the sixth harmonic
(6x the fundamental frequency). In the case of the Tri-Level Complex
Wave, however, the harmonic waves are not only frequency multiples,
they are also amplitude multiples of the fundamental, or hexagramatic wave.
Although this notion of wave harmonics may only be an interesting perspective
at this point, it may be useful when examining the wave features of these
number sets using Fourier analysis.
The Expansion Process Expressed Graphically
Graphically speaking the Trigramatic Complex Wave is simply a 3x magnification of the linear complex wave, i.e. the magnification of the first two of its simple wave cycles. This 3x magnification means that the linear complex wave segments are expanded by a factor of three, in both the x and y directions. Similarly, the Hexagramatic Complex Wave is a 6x magnification of the linear complex wave, i.e. the magnification of the first of the simple wave cycles. Figure 7 is a graphical representation of this process, and shows the 3x and 6x magnification over the first 64 transition index values (64 of 384). The graph shows one complete linear cycle, one-third of a trigramatic wave cycle, and one-sixth of a hexagramatic wave cycle.
One significant feature to notice in Fig. 7, is that the linear, trigramatic, and hexagramatic waves are offset from one another - the first peak of each wave level is not aligned with its neighbor. Notice also, that this first peak at each wave level (linear, tri, and hex) occurs at the primary closure point (i.e. the first closure point as observed from within the envelope of the linear, tri, and hex bi-directional waves). For the linear wave this closure occurs at index 1, for the trigramatic wave it is at index 3, and for the hexagramatic wave it occurs at index 6. This is exactly the defining 1-3-6 ratio for linear, trigramatic, and hexagramatic waves, which this graph illustrates well.
Another feature to notice about Fig. 7 is that this wave offset is due to the fact that linear wave segment 1 is included in the linear wave number set. Remember that this first segment (from index 0 to index 1) is a result of the "wrapping" feature of the simple Bi-directional wave - transition 64 is wrapped (copied) to transition zero for the simple wave, or transition 384 is

wrapped to zero for the entire linear bi-directional wave. Therefore, transition number 0 is not the starting point of the wave, but transition 1 is. Nonetheless, let us mathematically express the linear forward wave expansion, shown in Fig. 7, as follows:
Or by rearranging terms in [46]:
Likewise for the linear reverse wave:
and rearranging:
This same set of equations, [46] through [49] can be used to expand the linear wave into the hexagramatic wave shown in Fig. 7, by replacing all number 3's by 6's. However, since the actual starting point for this wave set is at transition 1 and not transition 0, the proper expansion will look as shown in Fig. 8. In this figure, alignment between linear, trigramatic, and hexagramatic waves occurs at transition index 1; also a point of primary closure.
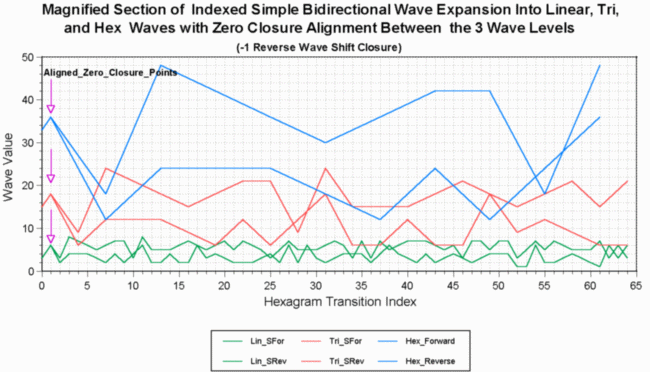
Fig. 8 also shows this expansion in terms of the linear,
tri, and hex bi-directional waves, in which the linear bi-directional
wave is expanded into the trigramatic, and hexagramatic bi-directional
waves. However, these bi-directional waves are eventually combined to form
the complex wave system, as described by equation [43] for the linear wave
case. Since all three bi-directional waves are to be expressed as complex
waves, several operational steps can be omitted and the process streamlined,
by expanding the linear complex wave directly. Consequently, we will follow
a mathematical process that expands the linear complex wave, described
by equation [43], into the tri and hex complex waves. In the interest of
maintaining visual clarity of this process, however, and of remaining true
to the notion of a directed flowing wave cycle at all three levels of expression,
we show the expanded wave system as bi-directional in nature.
Fig. 9 shows the proper expansion of the linear bi-directional wave into the trigramatic and hexagramatic bi-directional waves, with wave indexing at transition 1. This graph shows the entire 384 number wave domain, in which a single hexagramatic wave cycle contains two trigramatic wave cycles and six linear wave cycles. This notion of all three levels of wave expression being contained, or nested in one level is the actual theoretical basis for the tri-level wave combination that produces a single Tri-Level Complex Wave - the data set.
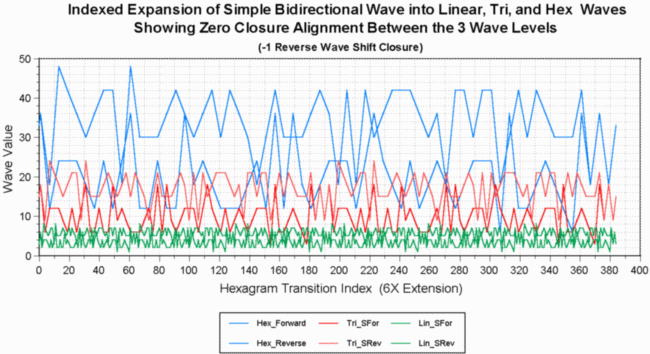
Fig. 10 shows the same tri-level bi-directional wave set as Fig. 9, but with the average value of the linear and trigramatic bi-directional waves aligned with the average value of the hexagramatic wave. These two figures are mathematically equivalent for this development, as we shall see.
Fig. 10 is included here because it is the form of the Tri-Level Bi-directional Wave that appears in the TWZ documentation, and it is obvious that it looks different than Fig. 9. The linear and trigramatic bi-directional waves in Fig. 10 have their average values aligned to the hexagramatic wave average value, so that they move about a common line - the hexagramatic average. This graph may look different than Fig. 9, but the fact is that they are identical mathematically. The reason is that, in order to produce the combined complex wave, the forward wave is subtracted from the reverse wave, as shown in equations [40] through [43]. Since the forward and reverse waves remain closed, or connected at their endpoints, it doesn't matter where

along the y-axis they are shifted - the resulting difference is the same. Consequently, Fig. 9 is equivalent to Fig. 10 and the graphs appearing in the TWZ documentation.
So let us now begin with the mathematical expansion of
the Linear Complex Wave, of equation [43], into the Trigramatic
and Hexagramatic Complex Waves, and then finally into the Tri-Level
Complex Wave - the 384 number data set.
[continue] [results & conclusions] [index] [hyperborea] [back]