(1) The TrigramaticComplex Wave                                                      [skip to next]

Close inspection of Figs 8 and 9 reveals the relationship between the functions describing the linear, trigramatic, and hexagramatic waves. The relationship between linear and trigramatic forward waves is shown in Figs 8 and 9, and is expressed mathematically as follows:

             [50]

Where the quantity within the parentheses is the argument for y( ), and not a multiplier. Rearranging terms in [50] we get:
 

             [51]

Where  is the value of the trigramatic forward wave at x, and  is three times the value of the linear forward wave at . Likewise, the trigramatic reverse wave is expressed in terms of the linear reverse wave by the equation:

             [52]

and by rearranging terms we get:

             [53]

The trigramatic complex wave is defined in the same manner as the linear complex wave, with the tri forward wave subtracted from the tri reverse wave as in equation [40] and expressed in trigramatic terms by:

             [54]

 
Using [50], [52], and [54] we can express the trigramatic complex wave in terms of the linear complex wave as follows:
 

             [55]

or equivalently:

             [56]

Factoring the right side of [56] gives:                              [57]

 
Substituting the expression for the linear complex wave on the right hand side of equation [40], into [57]:
 

             [58]

             [59]

Equation [59] shows that the value of the trigramatic complex wave at x, is equal to three times the value of the linear complex wave at . Replacing the x - term term in the  expression of equation [43] with the expression , then substituting into [59] gives us the defining equation of the trigramatic complex wave as follows:

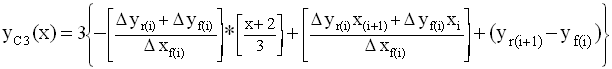         [60]

In this expression the subscript i is expressed as a function of x, using the process similar to that which produced equation [11]. In this case, since the x term has become , the expression defining the bounding subscript i then becomes:

             [61]

 
Where subscript i is renamed as j to distinguish it from the linear wave expression subscript shown in the previous linear wave equations. Equation [61] defines subscript j as the rounded down integer value of the function , thus establishing the boundary conditions for the trigramatic line segment mapped by this function.

Equation [60] expresses the Trigramatic Complex Wave (TCW) as an expansion of the Linear Complex Wave (LCW) directly. However, the same result would be obtained if the linear forward and reverse waves had been expanded into the trigramatic forward and reverse waves, and those results combined to for the trigramatic complex wave. This direct approach clearly eliminates two very detailed mathematical steps. The same series of steps will now be used to find the expression for the hexagramatic complex wave.
 

(2) The Hexagramatic Complex Wave

As for the trigramatic wave, inspection of Figs. 8 and 9 reveals that the relationship between the linear forward wave and the hexagramatic forward wave can be expressed:

             [62]

             [63]

Where  is the value of the hexagramatic forward wave at x, and  is six times the value of the linear forward wave at . Likewise, the hexagramatic reverse wave is expressed in terms of the linear reverse wave by the equation:

            [64]

and by rearranging terms we get:

             [65]

             [66]

 
Using [62], [64], and [66] we can express the hexagramatic complex wave in terms of the linear complex wave as follows:

             [67]

or equivalently:

             [68]

 
Factoring the right side of [68] gives:

             [69]

             [70]

then rearranging [70] we get:

             [71]

Equation [71] shows that the value of the hexagramatic complex wave at x, is equal to six times the value of the linear complex wave at . Replacing the x -term term in the  expression of equation [43] with the expression , then substituting into [71] gives us the defining equation of the hexagramatic complex wave as follows:

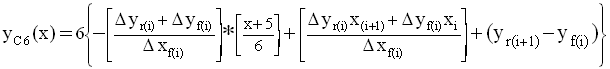         [72]

 
In this expression the subscript i is expressed as a function of x, using the process similar to that which produced equations [11] and [61]. In this case, since the x term has become , the expression defining the bounding subscript i then becomes:

             [73]

Where subscript i is renamed as k to distinguish it from the linear and trigramatic wave expression subscripts shown in the defining wave equations. Equation [73] defines subscript k as the rounded down integer value of the function , thus establishing the boundary conditions for the hexagramatic line segment mapped by this function.

As with the Trigramatic Complex Wave (TCW) expressed in [60], equation [72] expresses the Hexagramatic Complex Wave (HCW) as an expansion of the Linear Complex Wave (LCW) directly. Similarly, the same result would be obtained if the linear forward and reverse waves had been expanded into the hexagramatic forward and reverse waves, and those results combined to form the hexagramatic complex wave. With the linear [43], trigramatic [60], and hexagramatic [72] complex waves now defined mathematically and expressed graphically, we are now in a position to combine them to form the Tri-Level Complex Wave, or 384 number "data set".
 

(3) The Combined Tri-Level Complex Wave

Now that the three levels of TimeWave expression have been described and defined mathematically, we are now in a position to integrate these three levels into a single unitary system of expression. The Tri-Level Complex Wave is seen as an integrated whole, and analogous to the I-Ching hexagram that functions as a holistic entity, but contains the individual expression of hexagram, trigram, and line (yin or yang). In order to establish this tri-level expression mathematically, we combine the complex waves of the linear, trigramatic, and hexagramatic levels of expression. The general equation expressing the summation of the three wave levels is written as follows:
 

             [74]

Substitutions in [74] for lin(x), tri(x), and hex(x) from equation [43], [60], and [72] give us:
 

              [75]

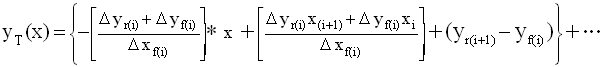
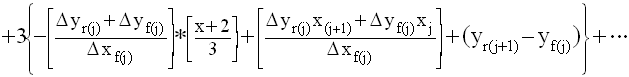
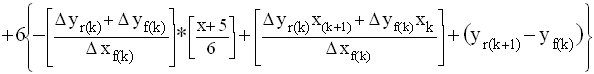             [76]

Equation [76] is the defining equation for the Tri-Level Complex Wave. This expression takes one from the individual elements of the linear complex wave, up to the trigramatic and hexagramatic complex waves, and finally to the tri-level complex wave. Notice that the subscripts j for the trigramatic section, and k for the hexagramatic section of equation [76] have replaced the subscript i in equations [60] and [72], as they have been defined in equations [61] and [73]. We now have a complete and well-defined function for our Tri-Level Complex Wave, or data set.

Equation [76] produces a tri-level wave number set that contains some negative values. The 384 number data set, on the other hand, is the set of positive real numbers in the domain . This means that part of the "raw" data set produced by equation [76] lies outside the y -value domain that is thought to be the proper expression of this waveform. One procedure that is widely used for converting negative values of some arbitrary waveform, into positive values, is the use of the absolute value operator. If one views this tri-level complex wave as some kind of information carrying signal, like an amplitude modulated radio wave, for example, then a valid procedure for processing such a signal is the application of the absolute value operator. In the rf signal processing case, the received modulated-carrier waveform is passed through absolute value circuitry (rectifier) so that the negative values of the wave are converted to positive values. This actually improves the signal to noise ratio of the carrier envelope, which is the information carrying modulation signal. This "rectified" signal is then processed by a detector circuit that extracts the information carrying modulation wave from the carrier wave. Although the tri-level wave and the radio wave are not strictly analogous, they appear similar enough to make a plausible argument for the application of the absolute value operator here. This operation is expressed as:

             [77]

 
Where:  is the Data Wave that is graphed in Fig. 11, and defined as the absolute value of the Tri-Level Complex Wave as expressed in equation [76]. This number set is used as input data for the TimeWave Zero software, which performs an infinite series expansion that Meyer calls a fractal transform [11] to generate the TimeWave viewed on the computer screen.
 

[continue]             [results & conclusions]             [index]             [hyperborea]             [back]